Quando você visita a página de Sangue & fogo na Amazon logo em baixo ela já nos recomenda por exemplo O Senhor dos Anéis ou O nome do vento. Isso ocorre porque outras pessoas que visitaram Sangue & fogo também visitaram O Senhor dos anéis ou O nome do vento, logo faz sentido indicá-los à você também.
É chamada de filtragem colaborativa porque a recomendação é baseada em outras pessoas, ou seja, as pessoas similares colaboram com a recomendação.
Como encontrar alguém similar?
Vamos começar com um exemplo, pois acredito que ajuda melhor a entender. Imagine que tenhamos avaliações de livros de várias pessoas. As avaliações são de diversos livros e vão de 0 a 5. Para simplificar vamos nos focar em dois livros específicos, o Livro I e o Livro II. Abaixo seguem algumas das avaliações.
| Ser vivo | Nota Livro I | Nota Livro II |
|---|---|---|
| Alan | 3 | 5 |
| Grace | 1 | 2 |
| Alonzo | 5 | 5 |
| Dijkstra | 4 | 1 |
Com apenas dois livros é possível plotar as avaliações em um gráfico 2D.
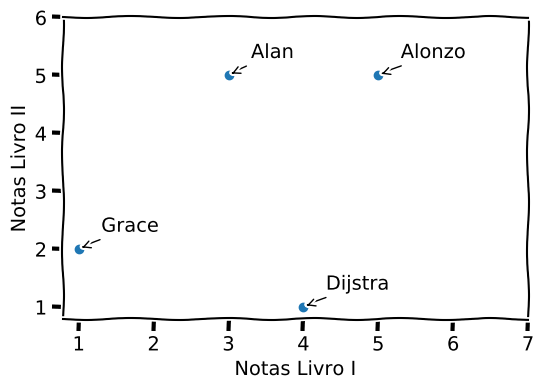
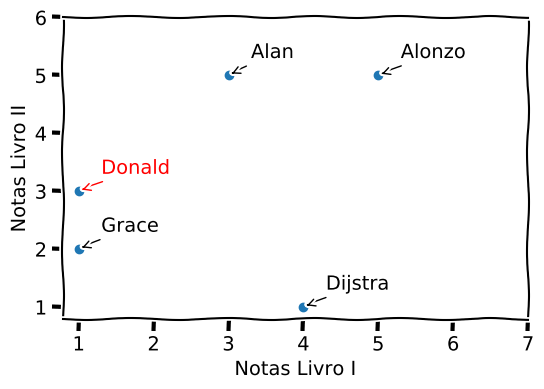
Se quisermos recomendar algum livro para um quinto usuário, Donald, que deu nota 1 para o Livro I e nota 3 para o Livro II, temos que primeiramente buscar pessoas que têm avaliações mais próximas à ele, calculando a distância entra as notas. Há várias formas de se calcular a distância entre dois pontos nas próximas seções veremos alguns métodos.
Distância de Manhattan
A Distância de Manhattan, também chamada de distância do taxi, é uma das formas mais simples de calcular a distância entre dois pontos. Ela é dada pelo módulo da diferença entre os valores de x somado com o módulo da diferença dos valores de y. Como é possível ver na expressão abaixo:
$$ d = | x_1 - x_2 | + | y_1 - y_2 | $$
Suponha que as avaliações do Alan sejam representadas por $(x_1, y_1)$ e as de Donald por $(x_2, y_2)$. A Distância de Manhattan dos dois é dada por:
$$ d = | x_1 - x_2 | + | y_1 - y_2 | $$
$$ d = | 3 - 1 | + | 5 - 3 | $$
$$ d = 2 + 2 $$
$$ d = 4 $$
Simples, não? Vamos ver graficamente o que significa essa distância:
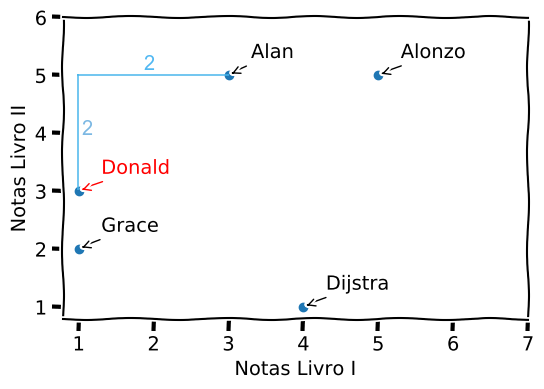
Para a Distância de Manhattan, a menor distância entre dois pontos é aquela que a soma das arestas que levam ao segundo ponto é a menor distância. No exemplo do Donald ao Alan, para sair do Donald e chegar ao Alan, o menor caminho é aquele que andamos duas unidades positivas em y e duas unidades positivas em x, não importando a ordem.
Seguem a distância do Donald até todos os outros usuários:
| Ser vivo | Distância até Donald |
|---|---|
| Alan | 4 |
| Grace | 1 |
| Alonzo | 6 |
| Dijkstra | 5 |
Como podemos ver acima, quem tem a menor distância até Donald é a Grace, logo se ela estiver avaliado muito bem o Livro VII, o qual Donald ainda não leu, podemos fazer a recomendação desse livro ao Donald.
Distância Euclidiana
A Distância Euclidiana considera que a menor distância entre dois pontos é a linha reta que une os dois. Com isso, podemos usar o saudoso Teorema de Pitágoras para fazer esse cálculo.
Teorema de Pitágoras
Achou que nunca iria usar o Teorema de Pitágoras depois da escola?
Como o Teorema de Pitágoras é muito difundido, irei deixar apenas o link para ajudar você a relembrar.
Queremos encontrar a distância euclidiana entre Alan e Donald, faremos um triângulo retângulo onde a hipotenusa é a distância que queremos encontrar.
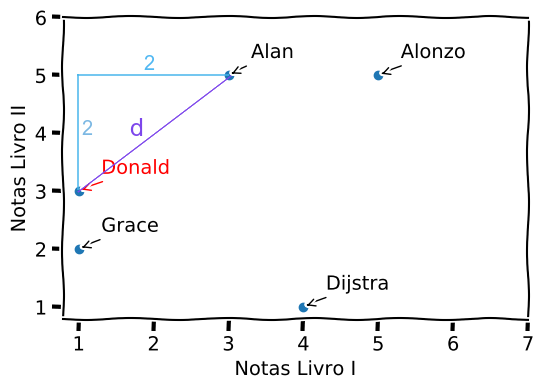
Sendo as avaliações do Alan representadas por $(x_1, y_1)$ e as de Donald por $(x_2, y_2)$. Vamos calcular a distância euclidiana dos dois:
$$ d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$
$$ d = \sqrt{(3 − 1)^2 + (5 − 3)^2} $$
$$ d = \sqrt{2^2 + 2^2} $$
$$ d = \sqrt{4 + 4} $$
$$ d = \sqrt{8} $$
$$ d = 2,83 $$
Usando a distância euclidiana tivemos um resultado bem diferente do da distância de Manhattan. Vamos calcular a distância euclidiana para as avaliações das demais pessoas.
| Ser vivo | Distância até Donald |
|---|---|
| Alan | 2,83 |
| Grace | 1 |
| Alonzo | 4.47 |
| Dijkstra | 3.60 |
Novamente Grace teve a menor distância até o Donald. Visualizando o gráfico, isso é perceptível para nós, mas o computador não tem essa percepção visual, por isso necessitamos dos cálculos. Vimos o cálculo para duas dimensões e como é feito na vida real, onde são muitas as dimensões?
N-dimensões
Além de comprar livros, outra coisa que fazemos é ouvir músicas. Há anos escuto música apenas
via streaming. Para quem utiliza o Spotify, o Daily Mix é um exemplo de listas criadas por algoritmos
de recomendação.
Para o próximo exemplo vamos imaginar que queremos fazer recomendações de artistas para diversas pessoas.
Cada uma das pessoas avaliaram algumas músicas de 1 a 5 estrelas, onde uma pessoa pode avaliar com
meia estrela para um artista, como 2.5 estrelas. Abaixo segue as avaliações, as avaliações com -
ocorrem quando a pessoa não ouviu e não avaliou o artista.
| Artista | Alan | Grace | Alonzo | Dijkstra | Donald | Malte |
|---|---|---|---|---|---|---|
| Eminem | 1.5 | - | 5 | 0.5 | 2.5 | 1.5 |
| Ramin Djawadi | 4.5 | 3.5 | 2.5 | 0.5 | - | 5 |
| Danheim | 3.5 | 1.5 | 4.5 | 0.5 | - | 5 |
| Armin van Buuren | 2.5 | 4.5 | - | 0.5 | 4 | 1 |
| Iron Maiden | 5 | 1 | 3.5 | 5 | 4 | - |
Temos um espaço de 6x5 dimensões, o que não é possível visualizar num gráfico 2D ou 3D. O que aplicaremos nessa seção pode ser generalizado para quaisquer dimensões.
Para dados com n-dimensões usamos a mesma abordagem de com duas. Como exemplo, vamos calcular a distância de Manhattan entre Alan e Malte:
| Artista | Alan | Malte | Diferença |
|---|---|---|---|
| Eminem | 1.5 | 1.5 | 0 |
| Ramin Djawadi | 4.5 | 5 | 0.5 |
| Danheim | 3.5 | 5 | 1.5 |
| Armin van Buuren | 2.5 | 1 | 1.5 |
| Iron Maiden | 5 | - | - |
| Distância de Manhattan | 3.5 |
Acima temos uma tabela que mostra o resultado para a distância de Manhattan, mas vamos calcular matematicamente também. Considere que as avaliações do Alan sejam dadas por $(e_1, r_1, h_1, a_1, i_1)$ e as do Malte por $(e_2, r_2, h_2, a_2, i_2)$, a distância de Manhattan é dada por:
$$ d = | e_1 - e_2 | + | r_1 - r_2 | + | h_1 - h_2 | + | a_1 - a_2 | $$
$$ d = | 1.5 - 1.5 | + | 4.5 - 5 | + | 3.5 - 5 | + | 2.5 - 1 | $$
$$ d = 0 + 0.5 + 1.5 + 1.5 $$
$$ d = 3.5 $$
Repare que como Iron Maiden não foi avaliado pelo Malte, ele não entra na conta. Agora vamos calcular a distância euclidiana:
| Artista | Alan | Malte | Diferença | Diferença^2 |
|---|---|---|---|---|
| Eminem | 1.5 | 1.5 | 0 | 0 |
| Ramin Djawadi | 4.5 | 5 | 0.5 | 0.25 |
| Danheim | 3.5 | 5 | 1.5 | 2.25 |
| Armin van Buuren | 2.5 | 1 | 1.5 | 2,25 |
| Iron Maiden | 5 | - | - | - |
| Soma dos quadrados | 4.75 | |||
| Distância Euclidiana | 2.18 |
Matematicamente temos:
$$ d = \sqrt{(e_1 - e_2)^2 + (r_1 - r_2)^2 + (h_1 - h_2)^2 + (a_1 - a_2)^2} $$
$$ d = \sqrt{(1.5 - 1.5)^2 + (4.5 - 5)^2 + (3.5 - 5)^2 + (2.5 - 1)^2} $$
$$ d = \sqrt{0^2 + 0.5^2 + 1.5^2 + 1.5^2} $$
$$ d = \sqrt{4.75} $$
$$ d = 2.18 $$
Generalização
Há uma única expressão que consegue generalizar a distância de Manhattan e a distância Euclidiana, é chamada de Métrica de Distância Minkowski ela é dada por: $$ d(x, y) = (\sum_{k = 1}^n |x_k - y_k|^r) ^ \frac{1}{r} $$
Quando $r = 1$ a distância de Minkowski se torna a distância de Manhattan e quando $r = 2$ se torna a distância de Euclides.
Manhattan: $$ d(x, y) = (\sum_{k = 1}^n |x_k - y_k|^r) ^ \frac{1}{r} $$
$$ d(x, y) = (\sum_{k = 1}^n |x_k - y_k|^1) ^ \frac{1}{1} $$
$$ d(x, y) = (\sum_{k = 1}^n |x_k - y_k|) $$
Euclides: $$ d(x, y) = (\sum_{k = 1}^n |x_k - y_k|^r) ^ \frac{1}{r} $$
$$ d(x, y) = (\sum_{k = 1}^n |x_k - y_k|^2) ^ \frac{1}{2} $$
$$ d(x, y) = \sqrt{(\sum_{k = 1}^n |x_k - y_k|^2)} $$
Quando r é zero, ela se aproxima da Distância de Hamming,
usada em problemas de classificação.
Considerando nosso exemplo, na expressão, $x$ e $y$ representam duas pessoas as quais estamos calculando a distância entre elas, $n$ é a quantidade de artistas que que ambas avaliaram. E como já dito, em $r$ definimos qual tipo de distância queremos. Quanto maior for o $r$, maior a diferença de uma dimensão influenciará a diferença total.
Chega de teoria por hoje. No próximo post vamos colocar implementar alguns algoritmos. Note que vimos nesse post algoritmos simples, futuramente estudaremos algoritmos mais complexos.
Não deixe de olhar as recomendações e as referências.
Recomendações
- Música: Avôhai - Versão Acústica
- Podcast: Café Brasil 699 - Um brasileiro (Me arrepiei umas 4 vezes ouvindo esse episódio.)
- Cerveja: Backer Medieval (Saudades.)
Créditos, referências e complementos
Anotações de um Padawan
Esse artigo é baseado nas minhas anotações de estudo, portanto não sou
expert no assunto e esse artigo está sujeito a erros.
Escrevo esse tipo de artigo com intuito de ajudar quem tem menos conhecimento
sobre o assunto do que eu, além de reforçar e facilitar meus estudos futuros.
Ao encontrar um erro, por favor, avise nos comentários que consertarei o mais breve possível.